Pressure Gradient Elastic Wave
The Process of Energy Transfer in Gases
Pressure Gradient Elastic Waves (PGEW)
are sound-type waves
that propagating
with sound velocity.
These waves are reflected,
are absorbed and
participate in interference process.
However, this type of wave
has unique properties.
The emergence of PGEW
leads to intense energy transfer
in a volume,
which manifests itself in the heating
and cooling of the walls.
The investigation of the phenomenon of energy transfer in gases
by Pressure Gradient Elastic Waves
was funded in 2014–2015 and 2020–2022
by the Ministry of Energy of Israel.
To carry out work on this project,
the company PG Wave Ltd. was created
We know that sound affects the temperature processes in gases.
Scientific articles have been published
describing the effects of sound on heating, on cooling, on drying.
The same class of phenomena includes temperature separation
in vortex tubes (Ranque effect)
and heating of the bottom of a cavity mounted opposite the nozzle
(Hartmann–Sprenger effect).
The operation of these devices is always accompanied by a loud sound.
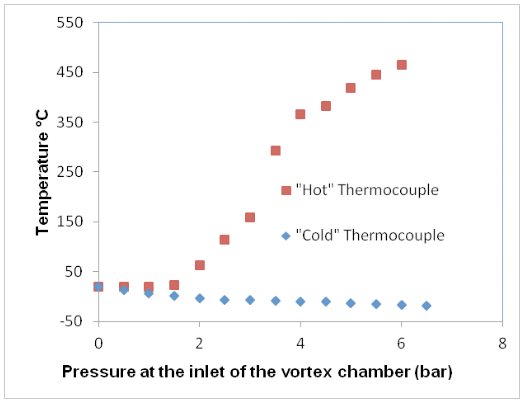
Dr. Beliavsky unexpectedly discovered temperature separation while working with a vortex chamber (Article 1).
The temperature at the periphery
reached + 465 °C and the temperature in the center decreased to ˗ 45°C
(air entered the vortex chamber at room temperature ~20°C).
Dr. Beliavsky unexpectedly discovered temperature separation while working with a vortex chamber (Article 1).
The temperature at the periphery
reached + 465 °C and the temperature in the center decreased to ˗ 45°C (air entered the vortex chamber at room temperature ~20°C).
This effect cannot be explained based on existed theories.
This circumstance prompted Dr. Beliavsky
to conduct additional investigations
to understand the physics of the phenomenon.
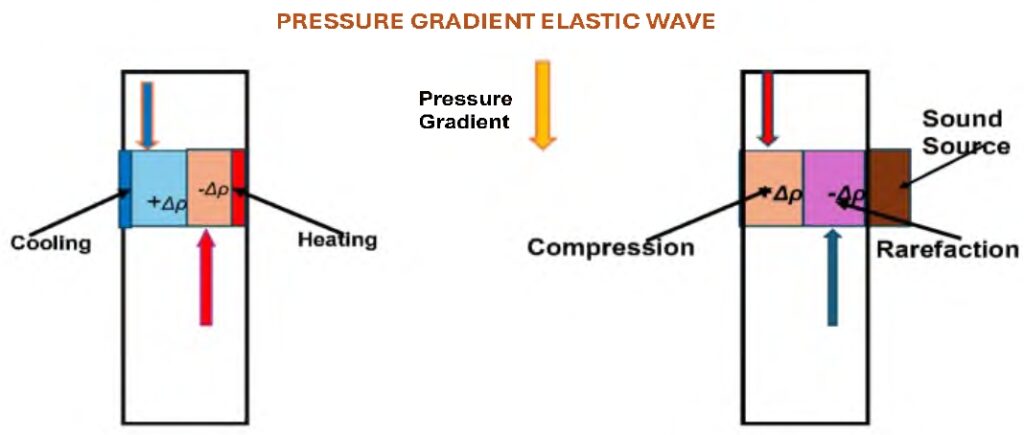
A fast density fluctuation always creates an elastic sound wave in a gas.
This position has been proven mathematically
(under the assumption of the occurrence
of a single disturbance of compression or rarefaction).
Rapid compression of a gas leads to its heating,
rapid expansion to cooling.
An ordinary sound wave represents a totality of individual
compression and rarefaction waves that alternate
and move at the velocity of sound away from the source of a wave
while the source oscillates or pulsates.
Heating in the compression wave is compensated
by cooling in the rarefaction wave,
so the temperature at any point in space does not change.
A PGEW occurs when three conditions are simultaneously satisfied in a region of space or a volume:
the volume is filled with a compressible fluid (gas).
there is a pressure gradient (gravity, rotation, acceleration, deceleration, etc.) inside a volume or region of space.
inside this volume, there are density fluctuations (powerful sound, turbulent pulsations).
Under these conditions,
the resulting pressure forces
act on the zones of sound (turbulent) density fluctuations
according to Archimedes law.
The action of these forces is faster than the speed of sound.
These forces additionally act on the gas,
creating a secondary disturbance and,
in accordance with Huygens principle,
create a secondary wave.
This is the Pressure Gradient Elastic Wave
However, these forces act on compression zones and rarefaction zones
in opposite directions.
PGEWs are a totality of compression waves
(that carry heat),
propagating in the direction of increasing pressure,
and a totality of rarefaction waves
(that carry cold),
propagating in the direction of decreasing pressure.
Justification for the existence of PGEW
does not require the introduction of new physical entities
and is based on classical thermodynamics,
more precisely on nonequilibrium thermodynamics
(systems with a pressure gradient
that arises under the influence of external forces).
The simplest way to justify the existence of PGEW is
an analogy with the well-known phenomenon of
natural convection
Consider the thought experiment.
а) b)
An elongated volume filled with a gas
in the presence of a pressure gradient
There are two elongated volumes filled with a gas, located in a force field that creates a pressure gradient (gravity, rotation…). The pressure gradient vector is directed from top to bottom
in the direction of increasing pressure.
In the left volume (a), plates are installed on the wall of the volume, which create heated and cooled microvolumes
in the adjacent space.
The theory of convection considers the balance of forces
acting on the boundaries of a microvolume
according to Archimedes’ law.
The resulting pressure force,
displacing the microvolume, will arise
when the density of the gas inside the microvolume differs
from the density of the surrounding gas.
Obviously, the cold microvolume (of higher density)
will shift in the direction of increasing pressure (down),
and the heated microvolume (of lower density)
will shift in the opposite direction.
In the right volume (b),
a sound source is installed on the wall of the volume,
which created a sound density fluctuation with the formation
of adjacent zones of compression and rarefaction.
Acoustic processes are studied within the framework
of classical thermodynamics,
so we can reasonably consider the balance of pressure forces acting on the boundaries of these zones
(just as in the phenomenon of convection).
According to Archimedes’ law, the resulting forces
acting on the compression and rarefaction zones of the sound wave are not equal to zero,
since the densities in these zones have shifted
from their equilibrium values.
These forces are directed along the pressure gradient vector.
The force acts on the compression zone in the direction of increasing pressure,
and on the rarefaction zone – in the opposite direction
– in the direction of decreasing pressure.
An important difference from the convection phenomenon discussed above
is the adiabatic nature of sound processes.
Therefore, the compression zone in the gas is heated,
and the rarefaction zone is cooled.
Pressure in gases is determined
by the average speed of molecules,
which is higher than the speed of sound.
Acoustic density fluctuations develop at the speed of sound.
These zones are subject to faster pressure forces,
creating an additional secondary density disturbance.
This secondary disturbance (according to Huygens’ principle)
necessarily creates a secondary elastic wave.
In accordance with the superposition principle,
this wave can be considered separately.
This is the Pressure Gradient Elastic Wave.
PGEWs consist of a compression front and a rarefaction front.
However, in accordance with the direction of the forces
that create sound disturbances in density,
the compression front of the PGEW
is directed towards increasing pressure,
and the rarefaction front of PGEW
is in the opposite direction
(towards decreasing pressure).
PGEWs occur at every point in the volume
within which density fluctuations have occurred.
This wave is a sequence of compression waves
propagating in the direction of increasing pressure,
and a sequence of rarefaction waves
propagating in the opposite direction.
In a limited volume the PGEWs heat the wall
delimiting the high-pressure zone
and cooled the wall (or region) of low pressure.
The PGEWs transfer energy from the low-pressure zone
to the high-pressure zone.
This energy transfer manifest
in the cooling of the low-pressure zone
and in the heating of the wall in the high-pressure zone.
The direction of heat transfer is determined by the pressure gradient vector.
PGEW is a unique natural heat pump
The PGEW concept explains the effects of Ranque and Hartmann–Sprenger, as well as other temperature effects in gases. Experimental results that cannot be explained without the involvement of PGEWs (Article 4) confirm this theory.
Understanding the physics of the phenomenon allows us to improve the characteristics of existing devices and create new ones that work using this PGEW principle.
Preliminary estimates suggest that these devices that operate on the PGEW principle will be significantly more economical than existing ones.
The results of this research
have been published in scientific articles
and reported at numerous scientific conferences.
What can PGEW give us?
A new class of Heat Pumps will be created that provide cooling and heating (such as in-home air conditioners). New devices can work using any gas. Freon will not be needed. This will reduce the influence of greenhouse gases on the climate.
Since the working medium in these Heat Pumps is gases, they can operate in any temperature range (including below 0°C). Thus, even with a low COP~2 value, these devices will allow 2 times to reduce electricity consumption for heating in winter in countries with cold climates (USA, Canada, Russia, northern Europe).
Understanding the physics of the PGEW phenomenon allows us to reasonably hope that these installations will be more effective than those used today. We set a goal to obtain a COP value of more than 4 for new heat pumps (today 2–3). This will provide significant savings in electricity consumption.


